Υπόθεση Riemann, στη θεωρία αριθμών, υπόθεση του γερμανού μαθηματικού Bernhard Riemann σχετικά με τη θέση των λύσεων στη συνάρτηση zem Riemann, η οποία συνδέεται με το θεώρημα πρωταρχικού αριθμού και έχει σημαντικές επιπτώσεις στην κατανομή των πρωταρχικών αριθμών. Ο Ρίμαν συμπεριέλαβε την υπόθεση σε μια εφημερίδα, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" ("Σχετικά με τον αριθμό των πρωταρχικών αριθμών λιγότερο από μια δεδομένη ποσότητα"), που δημοσιεύθηκε στην έκδοση Νοέμβριος 1859 του Monatsberichte der Berliner Akademie ("Μηνιαία κριτική της Ακαδημίας του Βερολίνου »).
Η συνάρτηση zeta ορίζεται ως η άπειρη σειρά ζ (s) = 1 + 2 + s + 3 −s + 4 −s + ⋯ ή, σε πιο συμπαγή σημειογραφία, , όπου η άθροιση (Σ) των όρων για n κυμαίνεται από 1 έως άπειρο μέσω των θετικών ακέραιων και s είναι ένας σταθερός θετικός ακέραιος μεγαλύτερος από 1. Η συνάρτηση zeta μελετήθηκε για πρώτη φορά από τον Ελβετό μαθηματικό Leonhard Euler τον 18ο αιώνα. (Για αυτόν τον λόγο, μερικές φορές ονομάζεται συνάρτηση Euler zeta. Για ζ (1), αυτή η σειρά είναι απλώς η αρμονική σειρά, γνωστή από την αρχαιότητα να αυξάνεται χωρίς δέσμευση - δηλαδή, το άθροισμά της είναι άπειρο.) Ο Euler πέτυχε άμεση φήμη όταν απέδειξε το 1735 ότι ζ (2) = π 2 /6, και ένα πρόβλημα που είχε ξεφύγει από τους μεγαλύτερους μαθηματικούς της εποχής, συμπεριλαμβανομένης της οικογένειας ελβετικό Bernoulli (Jakob, Johann, και ο Daniel). Γενικότερα, ο Euler ανακάλυψε (1739) μια σχέση μεταξύ της τιμής της συνάρτησης zeta για ακόμη και ακέραιους αριθμούς και των αριθμών Bernoulli, οι οποίοι είναι οι συντελεστές στην επέκταση της σειράς Taylor του x / (e x - 1). (Δείτε επίσης εκθετική συνάρτηση.) Ακόμα πιο εκπληκτικό, το 1737 ο Euler ανακάλυψε έναν τύπο που σχετίζεται με τη συνάρτηση zeta, ο οποίος περιλαμβάνει το άθροισμα μιας άπειρης ακολουθίας όρων που περιέχουν τους θετικούς ακέραιους αριθμούς και ένα άπειρο προϊόν που περιλαμβάνει κάθε πρωταρχικό αριθμό:
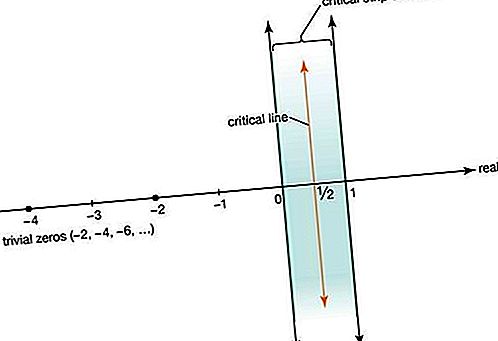
Ο Riemann επέκτεινε τη μελέτη της συνάρτησης zeta ώστε να συμπεριλάβει τους σύνθετους αριθμούς x + iy, όπου i = Τετραγωνική ρίζα του − 1, εκτός από τη γραμμή x = 1 στο σύνθετο επίπεδο. Ο Riemann γνώριζε ότι η συνάρτηση zeta ισούται με μηδέν για όλους τους αρνητικούς ακόμη και ακέραιους −2, −4, −6,
(τα λεγόμενα ασήμαντα μηδενικά) και ότι έχει έναν άπειρο αριθμό μηδενικών στην κρίσιμη λωρίδα σύνθετων αριθμών που πέφτουν αυστηρά μεταξύ των γραμμών x = 0 και x = 1. Ήξερε επίσης ότι όλα τα μη ασήμαντα μηδενικά είναι συμμετρικά ως προς το κρίσιμη γραμμή x = 1 / 2. Ο Riemann υπέθεσε ότι όλα τα μη-μηδενικά μηδενικά βρίσκονται στην κρίσιμη γραμμή, μια εικασία που στη συνέχεια έγινε γνωστή ως υπόθεση Ρίμαν.
Το 1914 Άγγλος μαθηματικός Godfrey Harold Hardy αποδείχθηκε ότι ένας άπειρος αριθμός των διαλυμάτων των ζ (s) = 0 υπάρχουν στην κρίσιμη γραμμή x = 1 / 2. Στη συνέχεια, αποδείχθηκε από διάφορους μαθηματικούς ότι ένα μεγάλο μέρος των λύσεων πρέπει να βρίσκεται στην κρίσιμη γραμμή, αν και οι συχνές «αποδείξεις» ότι όλες οι μη ασυνήθιστες λύσεις βρίσκονται σε αυτό είναι ελαττωματικές. Οι υπολογιστές έχουν επίσης χρησιμοποιηθεί για τη δοκιμή λύσεων, με τις πρώτες 10 τρισεκατομμύρια μη ασυνήθιστες λύσεις να φαίνεται ότι βρίσκονται στην κρίσιμη γραμμή.
Μια απόδειξη της υπόθεσης Ρίμαν θα έχει εκτεταμένες συνέπειες για τη θεωρία αριθμών και για τη χρήση των πρώτων στην κρυπτογραφία.
Η υπόθεση Ρίμαν θεωρείται εδώ και πολύ καιρό το μεγαλύτερο άλυτο πρόβλημα στα μαθηματικά. Ήταν ένα από τα 10 άλυτα μαθηματικά προβλήματα (23 στην έντυπη διεύθυνση) που παρουσιάστηκαν ως πρόκληση για τους μαθηματικούς του 20ου αιώνα από τον Γερμανό μαθηματικό David Hilbert στο Δεύτερο Διεθνές Συνέδριο Μαθηματικών στο Παρίσι στις 8 Αυγούστου 1900. Το 2000 ο Αμερικανός μαθηματικός Stephen Ο Smale ενημέρωσε την ιδέα του Hilbert με μια λίστα σημαντικών προβλημάτων για τον 21ο αιώνα. η υπόθεση Ρίμαν ήταν νούμερο ένα. Το 2000 ορίστηκε ένα πρόβλημα της χιλιετίας, ένα από τα επτά μαθηματικά προβλήματα που επέλεξε το Clay Mathematics Institute of Cambridge, Mass., US, για ένα ειδικό βραβείο. Η λύση για κάθε πρόβλημα της χιλιετίας αξίζει 1 εκατομμύριο δολάρια. Το 2008, ο Οργανισμός Προηγμένων Ερευνητικών Προγραμμάτων Αμυνας των ΗΠΑ (DARPA) το χαρακτήρισε ως μία από τις μαθηματικές προκλήσεις του DARPA, 23 μαθηματικά προβλήματα για τα οποία ζητούσε ερευνητικές προτάσεις για χρηματοδότηση - «Mathematical Challenge Nineteen: Settle the Riemann Hypothesis». Το Άγιο Δισκοπότηρο της θεωρίας των αριθμών."