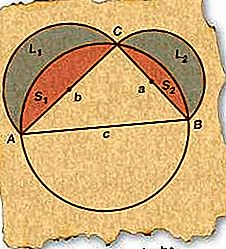
Ο Ιπποκράτης της Χίου (fl. 460 π.Χ.) απέδειξε ότι οι περιοχές σε σχήμα φεγγαριού μεταξύ κυκλικών τόξων, γνωστών ως θόλοι, θα μπορούσαν να εκφραστούν ακριβώς ως ευθύγραμμη περιοχή ή τετράγωνο. Στην ακόλουθη απλή περίπτωση, δύο λοβό που αναπτύσσονται γύρω από τις πλευρές ενός δεξιού τριγώνου έχουν συνδυασμένη επιφάνεια ίση με αυτή του τριγώνου.
-
Ξεκινώντας με το δεξί ΔABC, σχεδιάστε έναν κύκλο του οποίου η διάμετρος συμπίπτει με το AB (πλευρά c), την υποτείνουσα. Επειδή κάθε δεξί τρίγωνο που έχει σχεδιαστεί με διάμετρο κύκλου για την υποτελής χρήση του πρέπει να είναι εγγεγραμμένο μέσα στον κύκλο, το C πρέπει να βρίσκεται στον κύκλο.
-
Σχεδιάστε ημικύκλια με διαμέτρους AC (πλευρά b) και BC (πλευρά a) όπως στο σχήμα.
-
Επισημάνετε τους προκύπτοντες λοβούς L 1 και L 2 και τα προκύπτοντα τμήματα S 1 και S 2, όπως φαίνεται στην εικόνα.
-
Τώρα το άθροισμα των λοβών (L 1 και L 2) πρέπει να ισούται με το άθροισμα των ημικύκλων (L 1 + S 1 και L 2 + S 2) που τα περιέχουν μείον τα δύο τμήματα (S 1 και S 2). Έτσι, L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (αφού η περιοχή ενός κύκλου είναι π επί το τετράγωνο της ακτίνας).
-
Το άθροισμα των τμημάτων (S 1 και S 2) ισούται με την περιοχή του ημικύκλου με βάση το AB μείον την περιοχή του τριγώνου. Έτσι, S 1 + S 2 = π / 2 (c / 2) 2 - τριγώνου ABC.
-
Αντικαθιστώντας την έκφραση στο βήμα 5 στο βήμα 4 και παράγοντας κοινούς όρους, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Από ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, από το Πυθαγόρειο θεώρημα. Έτσι, L 1 + L 2 = ΔABC.
Ο Ιπποκράτης κατόρθωσε να τετράγωνα πολλά είδη λοβών, μερικά σε τόξα μεγαλύτερα και λιγότερο από ημικύκλια, και έδειξε, αν και ίσως δεν πίστευε, ότι η μέθοδος του μπορούσε να τετράγωνα έναν ολόκληρο κύκλο. Στο τέλος της κλασικής εποχής, ο Μποέθιος (περίπου 470–524 μ.Χ.), του οποίου οι λατινικές μεταφράσεις αποσπάσματα του Ευκλείδη θα κρατούσαν το φως της γεωμετρίας να τρεμοπαίζει για μισή χιλιετία, ανέφερε ότι κάποιος είχε ολοκληρώσει το τετράγωνο του κύκλου. Το αν η άγνωστη μεγαλοφυία χρησιμοποίησε λοβούς ή κάποια άλλη μέθοδο δεν είναι γνωστή, καθώς για την έλλειψη χώρου ο Boethius δεν έδωσε την επίδειξη. Μετέδωσε λοιπόν την πρόκληση του τετραγώνου του κύκλου μαζί με θραύσματα γεωμετρίας που φαίνονται χρήσιμα στην εκτέλεση του. Οι Ευρωπαίοι κράτησαν το άδικο καθήκον του Διαφωτισμού. Τελικά, το 1775, η Ακαδημία Επιστημών του Παρισιού, βαρεμένη με το καθήκον να εντοπίσει τις πλάνες στις πολλές λύσεις που της υποβλήθηκαν, αρνήθηκε να κάνει τίποτα περισσότερο με τους κύκλους.